Sonlu Elemanlar Yöntemiyle Doğal Taşınımla Isı Transferini Ele Alan Farklı Analizler

T.C.

TRAKYA ÜNİVERSİTESİ

MÜHENDİSLİK FAKÜLTESİ

MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ

SONLU ELEMANLAR YÖNTEMİYLE DOĞAL TAŞINIMLA ISI TRANSFERİNİ ELE ALAN FARKLI ANALİZLER

PROJE-3

1120201002 Selcen ÇALIŞKAN

DANIŞMAN: Yrd. Doç. Dr. Çiğdem SUSANTEZ

Mayıs 2017

EDİRNE

ÖZET

Bu projede COMSOL Multiphysics v4.3 programı kullanılarak 3 farklı çalışma yürütülmüştür. İlk olarak yatay bir silindirin önden görünüşü ele alınmıştır. İçerisinde hava dolaşan daire şeklinde kapalı ortamda farklı et kalınlıkları ve değişen yalıtım miktarlarının doğal taşınıma etkisinin 2 boyutlu analizi yapılmıştır. İkinci olarak; kare kesitli belirli kalınlıkta ve köşelerine eğim verilmiş, içinde hava dolaşan bir kapalı alan 2 boyutlu ele alınmıştır. Her iki çalışmada da sol taraf sıcak, sağ taraf soğuk kabul edilerek oluşan doğal taşınım mekanizması incelenmiştir. Son olarak üçüncü çalışmada, denklemler boyutsuzlaştırılarak programa yeniden girilmiştir. Bu çalışmada alt ve üst yüzeyleri yalıtımlı, yan yüzeyleri izotermal olan ve içerisinde karesel bir boşluk bulunduran, kare kesitli kapalı bir ortamda doğal taşınımla olan ısı transferi sayısal olarak incelenmiştir. Analizler iki boyutlu olarak ve daimi rejim için yapılmıştır. Rayleigh sayısının, içerdeki boşluğun konumunun,  ve  parametrelerinin ısı transferi üzerindeki etkileri incelenmiştir. Isı transferi üzerinde Rayleigh sayısının ve konumun önemli etkilere sahip olduğu görülmüştür.

ABSTRACT

In this project, 3 different studies were carried out using COMSOL Multiphysics v4.3 program. First, the front view of a horizontal cylinder was considered and 2D analysis of effects of different wall thicknesses and varying amounts of insulation on natural convection was carried out in a closed circular enclosure filled with air circulating inside. Secondly; the effect of varying wall thicknesses on the natural convection in a closed curved square cross-section enclosure filled with air circulating inside was analyzed as 2D. In both studies, the natural convection mechanism which is formed by considering the left side as hot and the right side as cold was examined. Finally, in the third study, the equations were dimensionless and the program was re-entered. In this study, the heat transfer with natural convection in a closed square enclosure with insulated bottom and top surfaces, isothermal side surfaces and a quadratic cavity was investigated numerically. The analyzes were done in two dimensions and for the permanent regime. The effects of the Rayleigh number, the position of the cavity, the   and  parameters on the heat transfer are investigated. The Rayleigh number and position on heat transfer have been found to have significant effects.

ÖNSÖZ VE TEŞEKKÜR

Bu projede 3 ayrı çalışma yürütülmüştür. 3 ayrı çalışma için de Comsol programı kullanılarak doğal taşınımla ısı transferi incelenmiştir.

İlk olarak daire şeklinde kapalı bir profil, daha sonra kare şeklinde kapalı bir profil ele alınmıştır. Bu iki çalışma için; taşınımla ısı transferinin gerçekleştiği duvarların sıcaklık değerleri ve ulaşılan maksimum hızlar çıkarılmıştır. Son aşamada kare profil için değerler boyutsuzlaştırılarak farklı parametreler için sonuçlar elde edilmiştir.

Bu projeyi yapmamda büyük emeği geçen ve her aşamada bana yardımcı olan Yrd. Doç. Dr. Çiğdem SUSANTEZ hocama teşekkürü bir borç bilirim.

Selcen ÇALIŞKAN

İÇİNDEKİLER

ÖZET…………………………………………………………………………………………………………………………i

ABSTRACT……………………………………………………………………………………………………………….ii

ÖNSÖZ VE TEŞEKKÜR……………………………………………………………………………………………iii

ŞEKİLLER DİZİNİ……………………………………………………………………………iv

TABLOLAR DİZİNİ………………………………………………………………………….vi

1. GİRİŞ………………………………………………………………………………………………………………………1

2. COMSOL………………………………………………………………………………………………………………..3

3. KONVEKSİYON İLE ISI TRANSFERİ ……………………………………………………………………..4

4. DOĞAL KONVEKSİYON MEKANİZMASI………………………………………………………………6

4.1. DOĞAL TAŞINIMIN ANA DENKLEMLERİ……………………………………………6

5. HAVAYLA DOLU YATAY SİLİNDİRDE DOĞAL TAŞINIMLA ISI TRANSFERİNİN İKİ BOYUTLU ANALİZİ……………………………………………..………………………..……….8

5.1. PARAMETRE VE DEĞİŞKENLERİN BELİRLENMESİ……………………………….9

5.2. FARKLI PARAMETRELERDE OLUŞAN HIZ DEĞERLERİ…………………………12

5.3. ORTALAMA SICAKLIK DEĞERLERİ…………………………………………………14

6. HAVAYLA DOLU KARE KESİTLİ KANALDAN DOĞAL TAŞINIMLA OLAN ISI TRANSFERİNİN 2 BOYUTLU ANALİZİ…………………………………………………….19

6.1. SONUÇLAR……………………………………………………………………………..23

7. BOŞLUKLU KARE KESİTLİ BİR ORTAMDA DOĞAL TAŞINIMLA ISI TRANSFERİNİN SAYISAL ANALİZİ………………………………………………………..25

7.1. BOYUTSUZ DEĞİŞKENLER VE BOYUTSUZ DENKLEMLER…………………………..27

7.2 SONUÇLAR………………………………………………………………………………28

KAYNAKLAR……………………………………………………………………………….30

ŞEKİLLER DİZİNİ

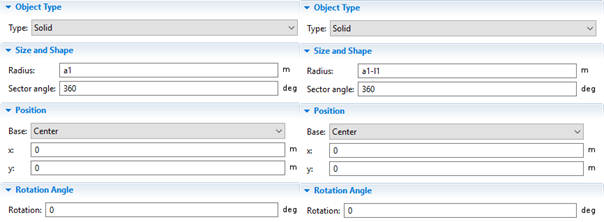
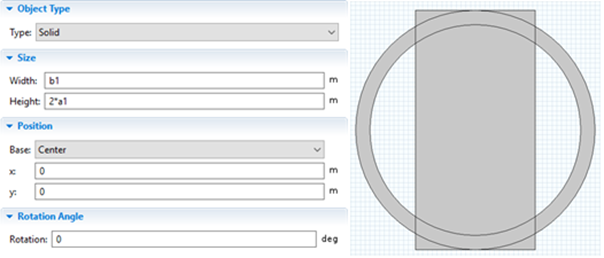
Şekil 5.1. Sırayla Circle-1(dıştaki), Circle-2(içteki), Rectangle İçin Girilen Değerler ve Oluşan Şeklin Geometrisi

Şekil 5.2. Parametric Sweep

Şekil 5.3. Thermal Insulation

Şekil 5.4. b₁= 0.4 m Yalıtım İçin Farklı Et Kalınlıklarında Hız Değerleri

Şekil 5.5. Line Average Değerleri

Şekil 5.6. b₁=0.4 İçin Tüm l₁ Değerlerindeki Sol ve Sağ Yüzeyler İçin Ortalama Yüzey Sıcaklık Değerleri (Yatay eksen data numarasını ifade eder. 1.data l₁=0.05 m, 2.data l₁= 0.06 m, 3.data l₁= 0.07 m, 4. data l₁= 0.08 m)

Şekil 5.7. b₁=0.5 İçin Tüm l₁ Değerlerindeki Sol ve Sağ Yüzeyler İçin Ortalama Yüzey Sıcaklık Değerleri (Yatay eksen data numarasını ifade eder. 1.data l₁=0.05 m, 2.data l₁= 0.06 m, 3.data l₁= 0.07 m, 4. data l₁= 0.08 m)

Şekil 5.8. b₁=0.6 İçin Tüm l₁ Değerlerindeki Sol ve Sağ Yüzeyler İçin Ortalama Yüzey Sıcaklık Değerleri (Yatay eksen data numarasını ifade eder. 1.data l₁=0.05 m, 2.data l₁= 0.06 m, 3.data l₁= 0.07 m, 4. data l₁= 0.08 m)

Şekil 5.9. b₁=0.7 İçin Tüm l₁ Değerlerindeki Sol ve Sağ Yüzeyler İçin Ortalama Yüzey Sıcaklık Değerleri (Yatay eksen data numarasını ifade eder. 1.data l₁=0.05 m, 2.data l₁= 0.06 m, 3.data l₁= 0.07 m, 4. data l₁= 0.08 m)

Şekil 5.10. b₁=0.8 İçin Tüm l₁ Değerlerindeki Sol ve Sağ Yüzeyler İçin Ortalama Yüzey Sıcaklık Değerleri (Yatay eksen data numarasını ifade eder. 1.data l₁=0.05 m, 2.data l₁= 0.06 m, 3.data l₁= 0.07 m, 4. data l₁= 0.08 m)

Şekil 5.11. Sol Yüzey İçin (yatay eksende data numaraları belirtilmiştir.)

Şekil 5.12. Sağ Yüzey İçin (yatay eksende data numaraları belirtilmiştir.)

Şekil 6.1. Geometrinin Son Hali İçin Square-1, Square-2 ve Fillet İçin Girilen Parametreler

Şekil 6.2. Variables

Şekil 6.3. Ortalama Yüzey Sıcaklığı

Şekil 6.4. Conjugate Heat Transfer Modulü

Şekil 6.5. Thermal Insulation

Şekil 6.6. Her Parametre İçin h_cold Değerleri

Şekil 6.7. Farklı l₁ Kalınlıklarında Sıcak Yüzey Sıcaklıkları

Şekil 6.8. Farklı l₁ Kalınlıklarında Soğuk Yüzey Sıcaklıkları

Şekil 6.9. Farklı l₁ Değerlerinde Hız Dağılımları

Şekil 7.1. Line Average

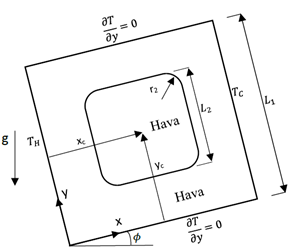
Şekil 7.2. Boşluklu Kare Kesitli Muhafaza

TABLOLAR DİZİN

Tablo 5.1. Hava ve Cam Elyaf İçin Parametrelerde Girilen Değerler

Tablo 5.2. Diğer Parametre Değerleri

Tablo 5.3. b₁= 0.4 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

Tablo 5.4. b₁= 0.5 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

Tablo 5.5. b₁= 0.6 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

Tablo 5.6. b₁= 0.7 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

Tablo 5.7. b₁= 0.8 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

Tablo 6.1. Parametrelere Girilen Değerler

Tablo 6.2. Parametrelerde Girilen Diğer Değerler

Tablo 6.3. Farklı l₁ Değerlerinde Oluşan Maximum Hız Değerleri

Tablo 7.1. Temel Denklemler ve Sınır Şartları

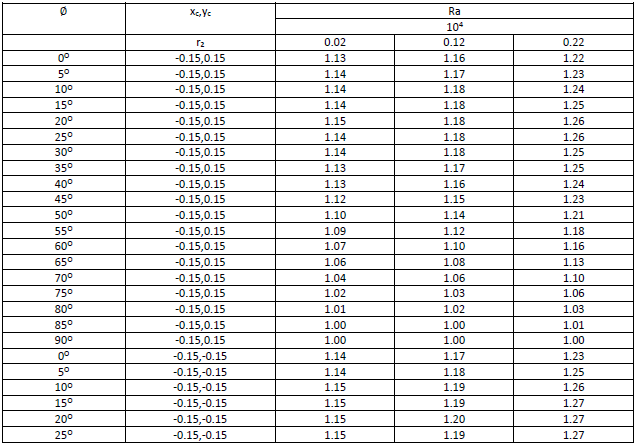
Tablo 7.2. x=0, y=0 Konumunda, r₂=0.02, 0.12 ve 0.22 Radius Değerlerinde ve ϴ=0^o-90^o Aralığında Farklı Rayleigh Sayıları İçin Elde Edilen Nusselt Değerleri

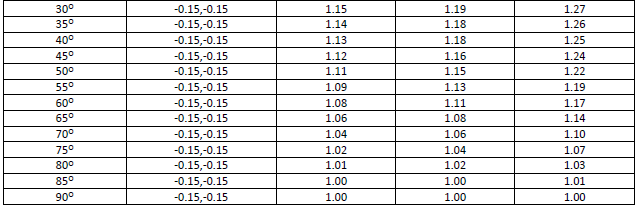
Tablo 7.3. Farklı konumlarda, r₂=0.02, 0.12 ve 0.22 Radius Değerlerinde ϴ=0^o-90^o Aralığı İçin Elde Edilen Nusselt Değerleri

1. GİRİŞ

Taşınım, katı yüzey ile akışkan arasında gerçekleşen bir tür ısı transferi çeşididir. Doğal taşınım ise, içerisinde oluşan sıcaklık farkı sebebiyle akışkanın hareket etmesi (ısınan havanın yoğunluğu azalır ve yükselir) ile ortaya çıkan taşınımdır.

Doğal taşınımla ısı transferi üzerine yapılan çalışmaların sayısı, 1980 yılı sonrası bilgisayarların kullanılmasıyla artmıştır. Altaç ve Uğurlubilek [1], iki ve üç boyutlu dikdörtgen muhafazalarda kararsız türbülanslı doğal konveksiyon ile ısı transferini sayısal olarak incelemiştir. Kararsız manyetohidrodinamik konveksiyon, ferroakışkan ile doldurulmuş yarım daire şeklinde bir muhafaza için sayısal ve istatistiksel teknikler kullanılarak Rahman ve Mojumder [2] tarafından analiz edilmiştir. İçi iletken bir katı gövde ile bitişik duvarları ısıtılmış ve soğutulmuş kare bir mahfazada eşlenik ısı transferi Lima ve Ganzarolli [3] tarafından çalışılmıştır. Hussain ve Jabbar [4] çalışmalarında, sinüzoid oluklu muhafazada yalıtılmış eğik merkezli perdeleme ve oluklanma frekansının sabit doğal konveksiyona etkisini araştırmıştır. Altac ve Bocu’nun [5] yapmış olduğu çalışmada, aktif duvara pimlenmiş 3B dikdörtgen hava dolu muhafazalarda laminer doğal konveksiyonla ısı transferi nümerik olarak incelenmiştir. Doğal konveksiyona tabi tutulmuş kapalı bir sıvı içine yerleştirilen katı engellerden kaynaklanan akış etkileşiminin, akış deseni ve ısı transferi üzerinde muazzam bir etkisi olabileceği Lage ve Junqueira [6] tarafından incelenmiştir. Gholizadeh ve Nikbakhti [7] tarafından yapılan, aktif sağ yan duvarı kısmi ısıtılmış trapezoid bir muhafaza içerisindeki çift difüzif doğal konveksiyon ile ilgili bir çalışma, sonlu fark yöntemi kullanılarak sayısal olarak yürütülmüştür.  Bir kare muhafaza içindeki eş değer ısıtılmış farklı ebatlarda eşkenar üçgen silindirlerin etrafındaki havadanın doğal konveksiyona bağlı ısı transferi ve akış analizi Sahu ve Singh [8] tarafından gerçekleştirilmiştir. Zamanla değiştiği öngörülen sıcaklıklara maruz bırakılan duvarlarda buharlaşma veya yoğunlaşmayı içeren, nemli hava ile dolu muhafazalarda ısı ve kütle transferi ile kombine geçici doğal konveksiyon Costa [9] tarafından sayısal olarak incelenmiştir. Bir tarafı yüksek sıcaklıkta, tavan kısmı düşük sıcaklıkta olan ve diğer yüzeyleri yalıtılmış iki boyutlu kapalı ortam için doğal taşınım problemi, akım fonksiyonu vortisite formülasyonu kullanılarak değişik en/boy oranlarında ve Rayleigh sayısının 10³-10⁷ aralığında olması durumları için Aydın ve Ünal [10] tarafından çalışılmıştır. De la Cruz ve Ramos [11], zaman bağımlı doğal taşınım olayını akış oluşturacak şekilde değişken sıcak ve soğuk sıcaklıklara sahip olan iki boyutlu kapalı ortamlarda incelemişlerdir. Böylece üst ve alt duvarları periyodik olarak ısıtılan ve soğutulan iki boyutlu kapalı ortamlar için geliştirilen doğal taşınım eşitlikleriyle sayısal bir çözüm yapılmıştır. Corcione [12], alttan ısıtılmış ve üstten soğutulmuş, yan duvarları farklı sınır şartlarındaki iki boyutu kapalı ortamlarda meydana gelen doğal taşınımla ısı transferini sayısal olarak incelemiştir. Kare geometriye sahip kapalı bir ortamdaki laminer doğal taşınım problemi çözümleri Davis ve Jones [13] tarafından karşılaştırmalı olarak verilmiştir. Karşılaştırma, değişik Rayleigh sayılarında elde edilen sonuçlar için yapılmıştır. Yüzey sıcaklığı zamanla periyodik olarak değişen düşey bir duvara sahip kapalı kare ortamdaki laminer doğal taşınımla ısı transferi olayı Kazmiercak ve Chinoda [14] tarafından sayısal olarak incelenmiştir. Sıcak olan yüzeyin sıcaklığı sinüzoidal şekilde değişmekte olup ortalama bir sıcaklık değeri civarında salınım yapmaktadır. Soğuk olan karşı duvar ise sabit bir sıcaklığa sahiptir. Kapalı ortam boyunca yüzey sıcaklığındaki değişimin akış ve ısı transferine etkisini farklı durumlar için elde etmişlerdir.

Bu projede farklı üç çalışma yürütülmüş olup ilk olarak; alt ve üst kısmından belirli ölçülerde yalıtılmış sol taraftan ısıtılan ve sağ taraftan soğutulan daire şeklinde içerisinde hava dolaşan 2 boyutlu kapalı ortam için doğal taşınımın farklı et kalınlıkları ve değişen yalıtım miktarlarında analizi yapılmıştır. İkinci olarak; 2 boyutlu kare kesitli belirli kalınlıkta içinde hava dolaşan bir kapalı alan ele alınmıştır. Bu 2 boyutlu alanın köşelerine belli bir eğim verilmiştir, tavan ve tabanı yalıtılmıştır. Sol taraf T_hot ve sağ taraf T_cold olarak belirlenmiştir ve bu sıcaklık farkı sebebiyle meydana gelen doğal konveksiyonun laminar akış durumunda farklı et kalınlıkları için analizi yapılmıştır. Üçüncü olarak; denklemler boyutsuz verilmiştir ve kare kesitli kapalı bir ortamda doğal taşınımla olan ısı transferi sayısal olarak incelenmiştir. Rayleigh sayısının, içerdeki boşluğun konumunun ve r_2 ve ϕ parametrelerinin ısı transferi üzerindeki etkileri incelenmiştir.

2. COMSOL

COMSOL Multiphysics®, fizik temelli problemleri modellemek ve simule etmek için geliştirilmiş sayısal yöntemlere dayanan, genel amaçlı bir yazılım platformudur. COMSOL Multiphysics ile, birleştirilmiş veya çoklu fizik olaylarını hesaplayabileceksiniz. Seçilebilecek 30’dan fazla eklenti ürünü ile simülasyon platformunu, elektrik, mekanik, akışkan akış ve kimyasal uygulamalar için özel fizik arayüzleri ve araçları ile daha da genişletebilirsiniz. Ek arabirim ürünleri, COMSOL Multifizik simülasyonlarınızı teknik hesaplama, CAD ve ECAD yazılımlarına bağlar. [15]

COMSOL Desktop®, uygulama alanından bağımsız olarak, birleştirilmiş bir iş akışı ile disiplinler arası ürün geliştirme için tasarlanmış güçlü bir entegre ortamdır. Eklenti modülleri COMSOL Multiphysics ile kesintisiz bir şekilde kaynaşmakta ve hangi eklenti ürünlerin kullanıldığına bakılmaksızın yazılımı çalıştırma şekliniz değişmeden kalmaktadır. Model Oluşturucu’daki model ağacı, modelin ve geometrisi, kafes, fizik ayarları, sınır koşulları, çalışmalar, çözenler, postprocessing ve görselleştirme işlevlerinin tümüne genel bir bakış sunar. COMSOL Multiphysics ile klasik fizik modellerini, eşzamanlı fizik fenomenlerini çözen çoklu fizik modellerine kolayca genişletebilirsiniz. Dahası, bu güce erişmek, matematik veya sayısal analiz konusunda derinlemesine bilgi gerektirmez. [15]

Sonlu elemanlar analizi, sonlu hacim yöntemi, sınır elemanı yöntemi ve parçacık izleme yöntemleri gibi eklenti modüllerinde birçok farklı yöntem kullanılır, ancak COMSOL Multiphysics’in önemi sonlu elemanlar yöntemi üzerindedir. Birçok sonlu elemanlar mevcuttur ve çözülme aşamasında yazılım tarafından tamamen birleşmiş elemanlar otomatik olarak üretilir. Sonlu elemanlar “on-the-fly” üreten bu patentli yöntem (COMSOL Multiphysics’e özgü) tam olarak sınırsız çoklu fizik kombinasyonlarına izin verir. [15]

COMSOL Multifizik, matematiksel ifadeler için dahili bir tercüman ile birlikte gelir. İfadeler daha sonra malzeme özellikleri, sınır koşulları veya kaynaklarda kullanılmak üzere değişkenlere atanabilir. Bu, çoğu zaman, özel ifadeye ihtiyaç duyulduğunda yazılımı uyarlamak için kod yazmanıza gerek kalmadığı anlamına gelir. [15]

3. KONVEKSİYON İLE ISI TRANSFERİ

Akışkan hareketiyle ilişkili olan ısı transferinin bu modu, akışkan içinde moleküllerin etkileşmesiyle gerçekleşen iletimle ısı transferi yanında akışkanın hareketi dolayısıyla enerjinin taşınması mekanizmalarının her ikisini de içerir. Sıvı veya gazı ısı taşıması için pompa veya fanla hareket ettiriyorsak bu zorlanmış taşınımdır. Birbirinden ayrılmış sıcak ve soğuk akışkanlar ısı transfer ekipmanlarına pompalanır. Isı transfer oranı akışkanların fiziksel özelliklerine ve akışa bağlıdır. Transfer edilen ısı akışkanları, akış hızıyla orantılı olduğu için zorlanmış (cebri) taşıma ile daha çok ısı transfer edilir. [16]

Eğer sıvı veya gazın sıcaklığındaki değişmeden dolayı yoğunluğu değişiyorsa ve bu değişim nedeniyle yaptığı hareket ile ısıyı taşıyorsa bu doğal taşınımdır. Örneğin; güneşli bir günde bir otomobilin metal kısımları, belli bir zaman diliminde, güneş ışınlarına maruz kaldığında güneş ışınımı dolaysıyla ısı transferine maruz kalacaktır. [16]

Otomobillerde bulunan metal aksam her yönde ışınım yaparak ısı kaybeder. Kaybolan ısı çevresindeki havayı ısıtır. Havanın otomobil üzerindeki hareketi ile doğal taşınım gerçekleşmiş olur. Otomobil hareket ettiğinde ise çevre havasına zorlanmış taşınımla ısı transferi gerçekleşecektir. Zorlanmış taşınımın, genelde, doğal taşınımdan çok daha fazla ısı transferine neden olduğu bilinmektedir. [16]

Konveksiyon, akışkan hareketi ile enerji taşınımı işlemidir. Ortam bir sıvı veya gaz ise, akışkan hareketi ile ısı enerjisi bir bölgeden diğer bölgeye sıcaklık farkından dolayı transfer edilecektir. Isı transferinin en önemli konusu konveksiyondur. Isı değiştirgeçlerinde akışkanlar, katı, cisimler (yüzeyler) ile birbirinden ayrılmış olduklarından, konveksiyon, bir yüzey ile akışkan arasında enerji taşınmasından en önemli ısı transferi mekanizmasıdır. [16]

Akışkan hareketi, taşınımla ısı transferinin ayırt edici özelliği olduğuna göre, ısı transferinin bu şekilde taşıyabilmek için akışkanlar mekaniği prensiplerinin iyi anlaşılmış olması gerekmektedir. Herhangi bir akışkan bir katı yüzey üzerinde akarken yüzey ile temas eden moleküllerin sürtünme ya da viskoz etkiler nedeniyle yüzeye yapışır. Yüzeye yapışan (yüzeyi ıslatan) bu moleküllerin yüzey üzerinde kaymadığı kabul edilirse burada akışkanın hızı sıfır olacaktır. [16]

Yüzey ile akışkan arasında birim zamanda ısı transferi şu şekilde hesaplanır:

Qt = h × A × (Ty − T∞)

(1)

Bu ifade 1701 senesinde Newton tarafından verilmiş olup, literatürde Newton’un Soğuma Kanunu diye adlandırılır ve konveksiyonun özel kanunudur. [16]

q_taş = Qt/A = h × (T_y − T_∞) (2)

h= Ortalama ısı taşınım kat sayısı (W/m²K) veya (yüzey ısı transferi kat sayısı). Bazı durumlarda ısı taşınım kat sayısının değeri analitik olarak bulunabilir, fakat çoğunlukla ölçümler sonucu tespit edilir. Isı taşınım kat sayısı, akış türü (laminar ya da türbülanslı), akışkan hızı, akışkan özellikleri, (viskozite, yoğunluk, ısı iletim kat sayısı vb.) sıcaklık, geometri gibi birçok etkene bağlı olarak değişir.

T_y = Yüzey sıcaklığı (ºC)

T_∞ = Bir kanal içerisindeki akışta akışkanların ortalama sıcaklığı veya bir yüzey üzerindeki akışta, yüzeyden uzaktaki sıcaklık. (ºC)

A= Sınır yüzey alanı (m²)

Q = Isı transferi (W)

q_taş = Isı akısı (W/m²)  [16]

4. DOĞAL KONVEKSİYON MEKANİZMASI

İyi bilinen birçok ısı transferi uygulaması, ısı transferinin öncelikli mekanizması olarak doğal taşınım içerir. Güç transistörleri, TV’ler, DVD’ler gibi elektronik aygıtların soğutulması; konvektör ısıtıcılar veya buhar radyatörlerinden olan ısı transferi; soğutma bobinleri ve güç iletim hatlarından olan ısı transferi bazı örneklerdir. [17]

Isı transferi çalışmalarında öncelikli değişken sıcaklıktır ve net kaldırma kuvvetinin sıcaklık farkları cinsinden ifade edilmesi istenir. Fakat bu özgül kütle farkının bir sıcaklık farkı cinsinden ifade edilmesini; bu ise sabit basınçta bir akışkanın özgül kütlesinin sıcaklıkla değişimini gösteren bir özelliğin bilinmesini gerektirir. Bu bilgiyi sağlayan özellik hacimsel genleşme katsayısı β’ dır. T sıcaklığında bir ideal gaz (P = ρRT) için β hacimsel genleşme katsayısı sıcaklığın tersine eşittir. [17]

βideal gaz = 1/T       (1/K)

(3)

4.1. DOĞAL TAŞINIMIN ANA DENKLEMLERİ

Navier-Stokes denklemleri non-lineer olup tam (exact) çözümleri kısıtlı sayıdadır. Ancak, çoğu halde bazı terimler ihmal edilerek daha basit denklemler elde edilebilir. Navier-Stokes denklemleri, aşağıdaki korunum kanunlarından türetilir:

•  Kütle

•  Enerji

•  Momentum

u: hız vektörü (m/s)

ρ: yoğunluk (kg/m³)

F_y: kaldırma kuvveti (N)

g: yer çekim ivmesi (m/s²)

μ: dinamik viskozite (Pa·s)

P: basınç (Pa)

5. HAVAYLA DOLU YATAY SİLİNDİRDE DOĞAL TAŞINIMLA ISI TRANSFERİNİN 2 BOYUTLU ANALİZİ

İlk olarak COMSOL Multiphysics v4.3 programı açılır. Çalışmamız 2 boyutlu olacağından 2D seçerek ilerleriz. Add Physics bölmesinden sırasıyla; Heat Transfer, Conjugate Heat Transfer, Laminar Flow “+” simgesine basılarak eklenir. Bir ileri daha gidilerek Stationary işaretlenir ve Finish simgesi tıklanarak bu aşama tamamlanır.

Bu aşama tamamlandıktan sonra sıra geometriyi oluşturma aşamasındadır. Geometride yatay silindirin önden görünüşüne sahip bir geometri oluşturabilmek için 2 circle seçeriz ve istediğimiz şekli meydana getirebilmek için iki dairenin farkını almamız gereklidir. Bunun için; geometry sağ tık yaparız ve şu işlemleri sırayla takip ederiz: boolean operations-difference. Yalıtım için ise rectangle seçeriz.

5.1. PARAMETRE VE DEĞİŞKENLERİN BELİRLENMESİ

Değerlerin programa tanıtılması aşamasında Global Definition sağ tıklanarak parametreler eklenir. Bu kısım ilerleyen aşamalarda bize kolaylık sağlaması içindir. Global Definition’da değerleri girdikten sonra uygun aşamalarda buradan değerleri çağırmak kolaylaşır. Global Definitions-Parameters kısmına girilen değerler Tablo 1.1 ve 1.2’ de gösterilmiştir.

Değerlerin programa tanıtılması aşamasında Global Definition sağ tıklanarak parametreler eklenir. Bu kısım ilerleyen aşamalarda bize kolaylık sağlaması içindir. Global Definition’da değerleri girdikten sonra uygun aşamalarda buradan değerleri çağırmak kolaylaşır. Global Definitions-Parameters kısmına girilen değerler Tablo 1.1 ve 1.2’ de gösterilmiştir.

Tablo 5.1. Hava ve Cam Elyaf İçin Parametrelerde Girilen Değerler

Malzeme	Hava (25 oC)	Cam Elyaf
k (W/m.K)	0.02514	0.043
c (J/kg.K)	1007	835
ρ (kg/m3)	1.204	16
µ (Pa.s)	0.00001825	–
Referanslar	[18]	[19]

Tablo 5.2. Diğer Parametre Değerleri

a1 (m)	0.5
l1 (m)	0.06
b1 (m)	a1
g (m/s2)	9.81
Tsoguk (oC)	10
Tsicak (oC)	50

Variables sütununda girilen değerler:

Beta = 1/(T+273.15) (1/K)

(13)

T_min = minop1(T) (K) (T_min değerini programın tespit etmesini istediğimizden sırayla; definitions-model couplings-minimum eklenip, geometri üzerinde yalıtımın dışında kalan sağ yüzey (soğuk yüzey) seçilir.)

Parametrelere gireceğimiz sıcak ve soğuk yüzeyin ısı taşınım katsayısı (h_sicak ve h_soguk) değerlerini bulurken, Nusselt’in [20] 1929’da içerisinde sıvı ya da hava olan yatay silindirler için analitik olarak belirlediği (10⁴ ≤ Gr_D.Pr ≤ 10⁸ aralığı için) formülasyonu kullanırız.

NuD = 0.502 (GrDPr)0.25

(14)

h_soguk hesaplarken T_yuzey = 30 ^oC kabulü yaparız ve T_soguk = 10 ^oC olduğuna göre;

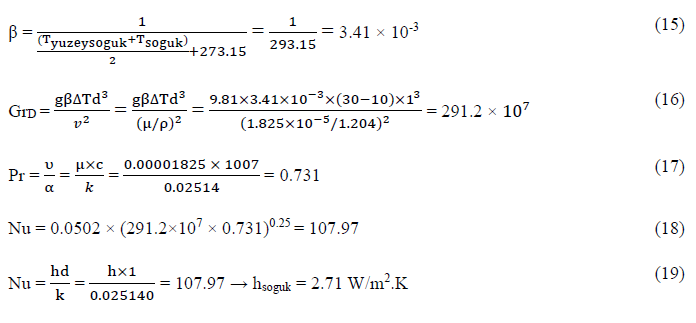
Sıcak yüzey için T_yuzeysicak = 40 ^oC ve T_sicak = 50 ^oC olduğuna göre yukarıdaki işlemleri sıcak yüzey için de hesaplarız ve h_sicak = 2.2325 W/m²K buluruz.

Daha sonra tüm bu değerler Conjugate Heat Transfer modülünde gireriz. Ek olarak bu modüldeki Volume Force kısmında kaldırma kuvvetinin formülünü girmemiz gerekir.

Fy = ρhava g β (T-Tmin)

(20)

İzolasyonun ve silindirin et kalınlığının ısı transferine etkisini ölçmek için Study kısmında Parametric Sweep ekleriz.

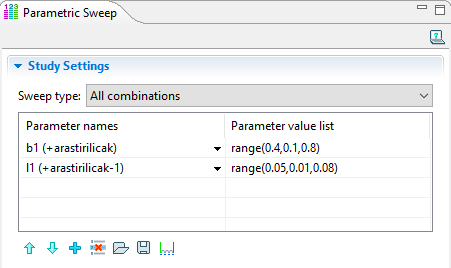
İzolasyonlu bölgeleri tanımlamak için; Conjugate Heat Transfer-Thermal Insulation kısmında izolasyonlu bölgeler seçilir.

Programı tüm bu işlemleri tamamladıktan sonra Study tıklayarak çalıştırırız ve sonuçları değerlendiririz.

5.2. FARKLI PARAMETRELERDE OLUŞAN HIZ DEĞERLERİ

Tablo 5.3. b₁= 0.4 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

l1 (m)	0.05	0.06	0.07	0.08
Maximum hız (m/s)	0.0956	0.0952	0.1004	0.0962

Tablo 5.4. b₁= 0.5 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

l1 (m)	0.05	0.06	0.07	0.08
Maximum hız (m/s)	0.0905	0.0935	0.0994	0.0925

Tablo 5.5. b₁= 0.6 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

l1 (m)	0.05	0.06	0.07	0.08
Maximum hız (m/s)	0.0869	0.0898	0.0935	0.0912

Tablo 5.6. b₁= 0.7 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

l1 (m)	0.05	0.06	0.07	0.08
Maximum hız (m/s)	0.0846	0.0886	0.0907	0.0868

Tablo 5.7. b₁= 0.8 İçin Tüm l₁ Değerlerindeki Ulaşılan Maximum Hızlar

l1 (m)	0.05	0.06	0.07	0.08
Maximum hız (m/s)	0.0833	0.0857	0.0843	0.0845

5.3. ORTALAMA SICAKLIK DEĞERLERİ

Sol yüzey (sıcak) ve sağ yüzey (soğuk) için ortalama değerleri okumak için, results-derived values sağ tıklanır ve average-line average eklenir. Daha sonra ortalaması alınacak yüzey (2 boyutta çizgi) seçilir. Seçilen yüzey eklendikten sonra tek tek tüm parametreler için değerler programa hesaplatılır.

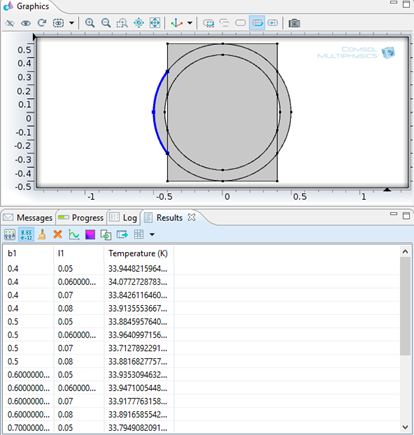
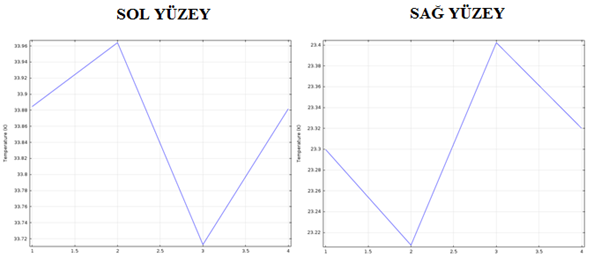
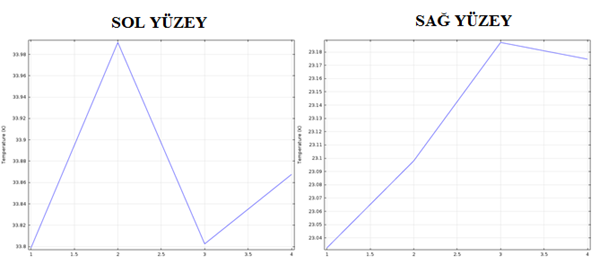
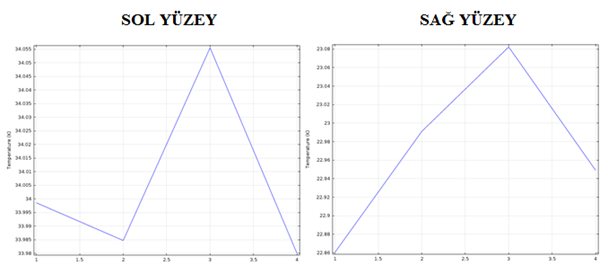
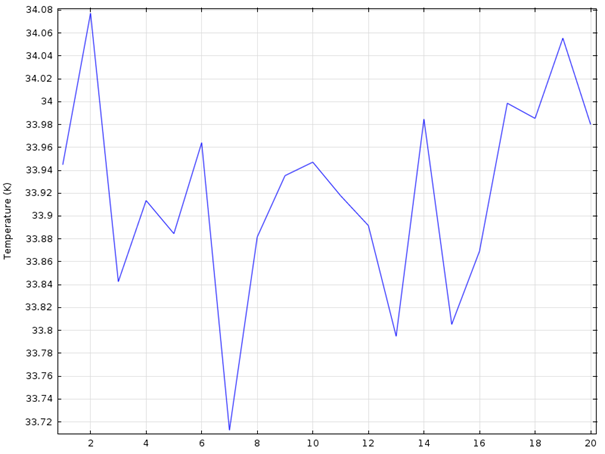
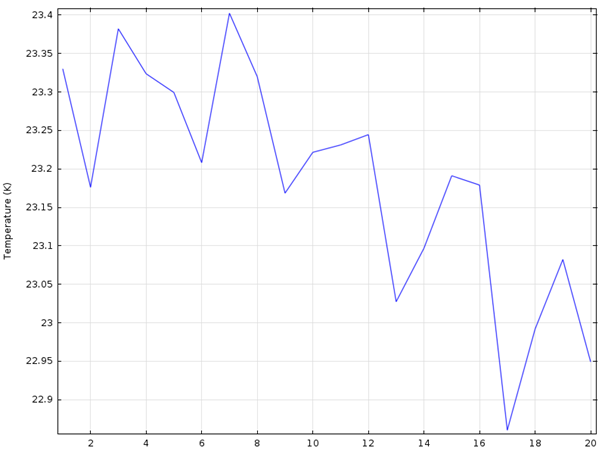
Isı transferinin en fazla gerçekleştiği optimum değerleri sol yüzeyde sıcaklığın en düşük olduğu değerler ve sağ yüzeyde sıcaklığın en yüksek olduğu değeri tespit ederek belirleriz. Buna göre sol yüzeyde düşülen minimum sıcaklık 7. değer olarak görülüyor ve bu değer b₁= 0.5, l₁=0.07 olduğu duruma denk geliyor. Aynı zamanda sağ yüzeyde çıkılan maksimum sıcaklık da aynı şekilde 7. değer olarak görülüyor ki bu da yaptığımız analizin doğruluğunu kanıtlıyor.

6. HAVAYLA DOLU KARE KESİTLİ KANALDAN DOĞAL TAŞINIMLA OLAN ISI TRANSFERİNİN 2 BOYUTLU ANALİZİ

Çalışmayı 2 boyutta yapacağımız için tekrar 2D seçerek ilerlenir. Add Physics bölmesinden sırasıyla; Heat Transfer, Conjugate Heat Transfer, Laminar Flow “+” simgesine basılarak eklenir. Bir ileri daha gidilerek Stationary işaretlenir ve Finish simgesi tıklanarak bu aşama tamamlanır.

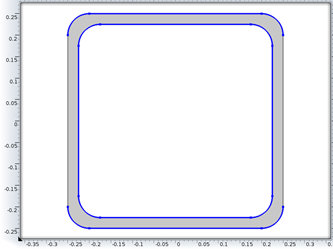
Bu aşama tamamlandıktan sonra sıra geometriyi oluşturma aşamasındadır. Geometride içi boş  kare kesit bir profil oluşturmak için geometry sağ tık yaparız ve 2 tane square eklenir ve tekrar geometry sağ tık yaparak şu işlemler sırayla takip edilir: boolean operations-difference. Daha sonra köşelere radius vermek için fillet eklenir ve şekil 6.1 oluşturulur.

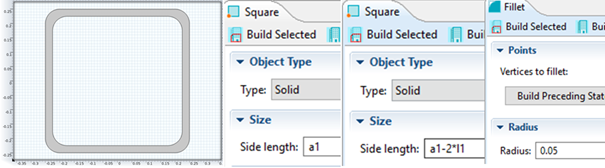
Geometri oluşturulduktan sonra parametre ve değişkenler atanır. Tablo 5.1’deki parametreler aynen girilir.

Tablo 6.1. Parametrelere Girilen Değerler

Malzeme	Hava (25 oC)
k (W/m.K)	0.02514
c (J/kg.K)	1007
ρ (kg/m3)	1.204
µ (Pa.s)	0.00001825
Referanslar	[18]

Tablo 6.2. Parametrelerde Girilen Diğer Değerler

a1 (m)	l1 (m)	g (m/s2)	Tcold (oC)	Thot (oC)
0.5	0.025	9.81	10	50

Parametre ve değişkenler programa tanıtılırken birimi Kelvin olan sıcaklık değerleri Celcius girilebilir; çünkü programın içerisindeki formüllerde yalnızca sıcaklık farkları geçtiğinden sıcaklığın hangi birimde girildiği önemsizdir. Yani bizim için önemli olan (ele aldığımız olgu) değişimdir.

Convective cooling’de girilecek olan h değerlerini programa hesaplatmak için formüller variables sütununa girilir.

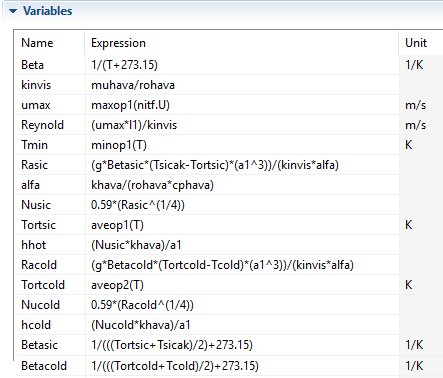
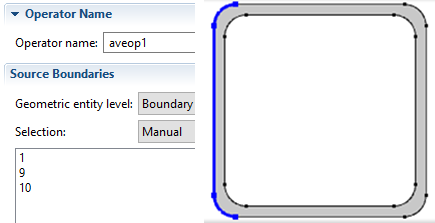
Maxop ve minop belirlenirken tüm yüzey, aveop1 için sıcak yüzey, aveop2 için ise soğuk yüzey seçilir ve eklenir.

Conjugate Heat Transfer modülünde bazı tanımlar yapılır. Bunlar; duvarlarda kaymama şartı, akışın gerçekleştiği bölgenin belirlenmesi, sıcak ve soğuk yüzeyle temas halindeki duvarların ısı taşınım katsayılarının belirlenmesi, başlangıç değerleri(T=20^oC) gibi tanımlamalardır.

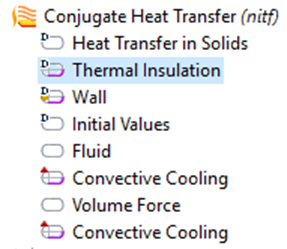
Tüm değerler girildikten ve şartlar belirlendikten sonra program bir kere çalıştırılır ve sonuçta derived values-line average eklenip soğuk ve sıcak yüzeyler seçilerek hcold ve hhot değerleri her parametre için evaluate denilerek programa hesaplatılır.

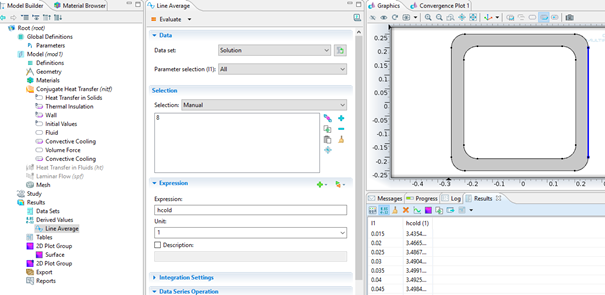
Tek bir hcold ve hhot değeriyle çalışmak istediğimizden her parametre için ortalama bir hcold ve hhot değeri sonuçlara bakarak kabul ederiz. Belirlediğimiz ortalama hcold değeri 3,49 W/m²K ve hhot değeri de 3,43 W/m²K’dir. Bu yeni değerleri bulduktan sonra parametrelere gireriz ve Convective Cooling’de değişiklik yaparak yeni belirlediğimiz ısı taşınım katsayısı değerlerini parametrelerden çağırırız.

6.1. SONUÇLAR

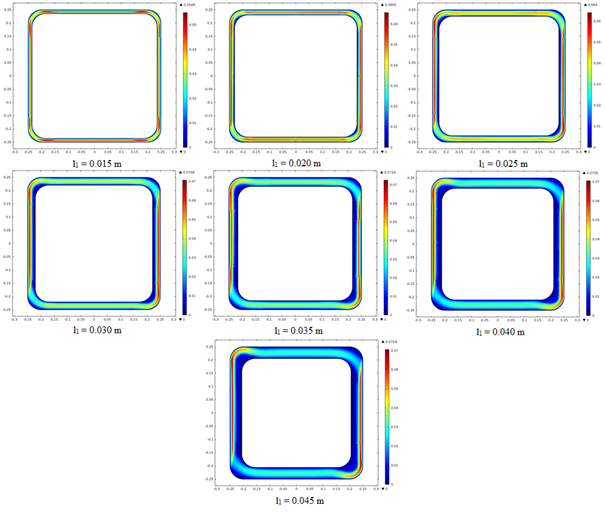
Tablo 6.3. Farklı l₁ Değerlerinde Oluşan Maximum Hız Değerleri

l1 (m)	Maximum hız (m/s)	Ortalama hız (m/s)
0,015	0,0549	0,0256
0,020	0,0655	0,0304
0,025	0,064	0,0268
0,030	0,0706	0,0248
0,035	0,0724	0,0229
0,040	0,0705	0,0205
0,045	0,0704	0,0192

7. BOŞLUKLU KARE KESİTLİ BİR ORTAMDA DOĞAL TAŞINIMLA ISI TRANSFERİNİN SAYISAL ANALİZİ

Bu çalışmada alt ve üst yüzeyleri yalıtımlı, yan yüzeyleri izotermal olan ve içerisinde karesel bir boşluk bulunduran, kare kesitli kapalı bir ortamda doğal taşınımla olan ısı transferi sayısal olarak incelenmiştir. Analizler iki boyutlu olarak, daimi rejimde yapılmıştır. Boyutsuzlaştırılan temel denklemler sonlu elemanlar ve simülasyon programı vasıtasıyla çözülmüş, Rayleigh sayısının, içerdeki karesel boşluğun konumunun, r_2 ve ϕ parametrelerinin ısı transferi üzerindeki etkileri incelenmiştir. Farklı parametrelerde program çalıştırılmış ve Derived Values-Line Average kısmında soğuk yüzey seçilerek Expression olarak -Tx (Nusselt sayısı) değerlerini karşılaştırırız. Nusselt sayısı, bir akışkan tabakasındaki taşınımın iletime oranı olduğundan, bu tabakadaki ısı transferinin ne kadar iyi olduğunu bu orana bakarak yorumlayabiliriz. Nusselt sayısı ne kadar büyük olursa hedeflediğimiz taşınım da o kadar etkili olur.

Tablo 7.1. Temel Denklemler ve Sınır Şartları

7.1. BOYUTSUZ DEĞİŞKENLER VE BOYUTSUZ DENKLEMLER

Boyutsuz Değişkenler:

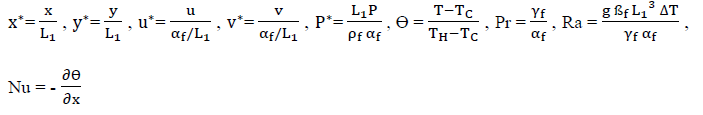
7.2. SONUÇLAR

Tablo 7.2. x=0, y=0 Konumunda, r₂=0.02, 0.12 ve 0.22 Radius Değerlerinde ve ϴ=0^o-90^o Aralığında Farklı Rayleigh Sayıları İçin Elde Edilen Nusselt Değerleri

Tablo 7.3. Farklı konumlarda, r₂=0.02, 0.12 ve 0.22 Radius Değerlerinde ϴ=0^o-90^o Aralığı İçin Elde Edilen Nusselt Değerleri