C Programlama Dilinde Nümerik İntegral Hesabı

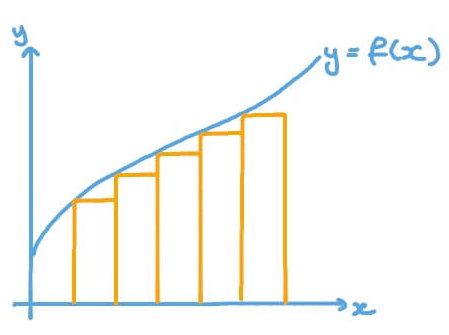
Resimde görüldüğü üzere nümerik integral almanın bir yöntemi olan Riemann toplamı yöntemi integral almak istenen fonksiyon aralığını dikdörtgenlere bölerek dikdörtgenlerin alanını toplama ile yapılır. Aşağıdaki c kodlarında başlangıç değişkeni integralin başlangıç noktasını, artış dikdörtgenlerin x eksenindeki uzunluğunu yani bulunacak sonucun gerçeğe yakınsamasını, son nokta integralin son noktasını, for döngüsü içerisindeki x=a*a integral alınmak istenen fonksiyonu belirtiyor. Kodumuzda a^2 fonksiyonunun 0 ile 10 aralığında integralini alıyoruz. a^2 fonksiyonun analitik çözümü (a^3)/3 = (10^3)/3 = 333,3333333333333333 ‘dür. Programı çalıştırdığımızda ise 0.00000001 artış değeri için bulunan integral 333.3333209307022571010748 dir. Artış değerini ne kadar azaltırsak sonuç gerçeğe o kadar yakınsamaktadır.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
double main()
{
    double baslangic=0;
    double artis=0.00000001;
    double sonnokta=10;
//////////////////////////////////////////////
    double c=0;
    double x;
    double b;
    double a;
    for(a=baslangic;a<=sonnokta;a=a+artis)
    {
        x=a*a;
        b=artis*x;
        c=c+b;
    }
    printf("Integral:%.25g\n",c);
    system("pause");
}