Dik tankın içindeki su seviyesinin (h) değişmeden kalması için tanka doldurulacak sıvı debisi ne kadar olmalıdır?
Yukarıdaki gibi bir problemi hızlıca hesplamak isteyeceğinizi düşünerek pythona aktarmak istedim. Aşağıdaki problemi referanslarda belirttiğim çok faydalı bir siteden ekliyorum:
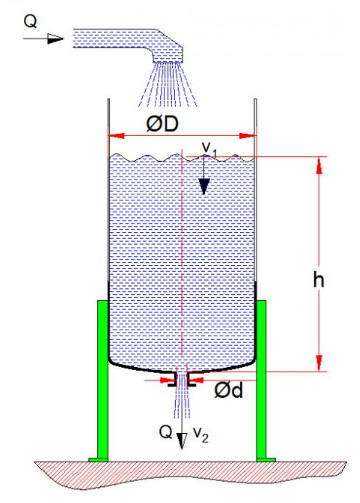
| Dik tankın içindeki su seviyesinin (h) değişmeden kalması için tanka doldurulacak sıvı debisi ne kadar olmalıdır.Bu problem basit ama sık karşılaşılan bir problem olduğu için vermekte yarar gördüm.Tank seviyesinin sabit kalması için giriş ve çıkış su debileri eşit olmalıdır. Aksi halde tank taşar veya seviyesi düşer. |
| Yani ; ( π D2 / 4) *V1 = ( π d2 / 4) *V2 Bu formülden V1=(d/D)2*V2 (Formül 1) Not: Tankın üst yüzeyinde belli bir kinetik enerji olması nedeni ile seviye değişmese bile V1 hızı sıfırdan büyüktür Bu tip problemlerde her zaman kullanılan denklem meşhur Bernoulli denklemidir.(Bkz.Önemli formüller) P1 +(1/2) ρV12 + ρ g Z1 = P2 +(1/2) ρV22+ ρgZ2 Problemimizde tank atmosfere açık olduğu ve atmosfere açık bir yere boşaltma yaptığı için P1=P2 dir Denklemi sadeleştirirsek (1/2) ρV12 + ρ g( Z1 – Z2) = (1/2) ρV22 Seviye farkı h olduğu için denklem aşağıdaki formu alır (1/2) ρV12 + ρ g h = (1/2) ρV22 (Formül 2) Yukarıda bulunan Formül 1 ve Formül 2 yi birlikte tanktan boşalma hızı V2 için çözersek |

olarak bulunur.
Şimdi bu tip bir problemi python da nasıl tanımlarız buna bakalım:
import math
print("dik tankın içindeki su seviyesinin (h) değişmeden kalması için tanka doldurulacak sıvı debisi ne kadar olmalıdır.")
while True:
D=input("Tankın çapını giriniz: ")
D=float(D)
d=input("Tankın çıkış deliği çapını giriniz: ")
d=float(d)
h=input("Tankın içindeki su seviyesi yüksekliği: ")
h=float(h)
a=math.pi*math.pow(d,2)/4
v2=math.sqrt(2*9.8*h/(1-(d/D)**4))
q=a*v2
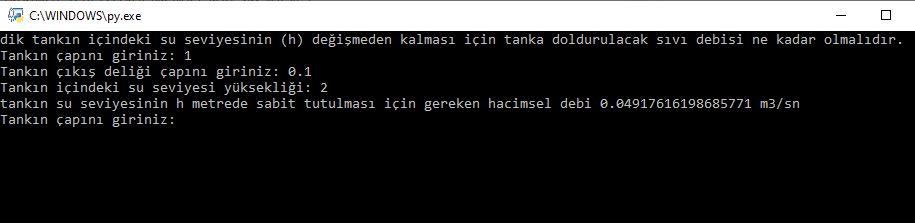
print("tankın su seviyesinin h metrede sabit tutulması için gereken hacimsel debi",q,"m3/sn")Öncelikle bir takım işlemleri hızlı şekilde tanımlamak adına math kütüphanesini ekliyoruz; daha sonra sorumuzu ekrana yazdırıyoruz(programı tanıtmak maksatlı). Daha sonra istediğimiz sonucu aldıktan sonra programın devamlı çalışaması adına sonsuz döngü tanımlıyoruz. İlk olarak tank çapı değerini kullanıcıya soruyoruz. ( Girilen tüm değerleri MKS birim sisteminde düşününüz. ) Daha sonra çap değeri atadığımız D’yi float olarak tanımlıyoruz. Aynı şekilde tankın çıkış delik çapını ve tank içerisindeki su seviyesi yükseklik değerini soruyoruz. Yukarıdaki formulleri belirle bir değere atıyoruz. Sonuçta gereken hacimsel debiye ulaşıyoruz. Kodlarımızın doğruluğunu aşağıdaki örnek ile doğrulayalım:
ÖRNEK
Çapı 1 metre olan tank içideki su seviyesinin 2 metre de sabit tutulması isteniyor.
Tankın çıkış deliği çapı 0.1 metre olduğuna göre tanka dakikada doldurulması gereken su kaç litredir?
D=1 metre, d=0.1 metre, h=2 metre

Yukarıda verilen problemde tank çapı D çıkış çapı d ölçüsünden 10 misli fazla ise tank yüzeyi hızı V1 sıfır kabul edilebilir.
V1 sıfır kabul edildiği zaman bernouli denkleminden
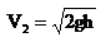
olarak bulunurdu. Bu durumda örnek problemde ki Q için sonuç hemen hemen aynı olur.
Aşağıdaki problem için kodlarımızı oluşturalım:
Q= Boşalma debisi (m3/sn)
V= Tankın sıvı ile dolu
kısmının hacmi (m3)
A= Tankın kesit alanı (m2)
h= sıvı seviyesi (m)
t= boşalma zamanı (sn)
A0= çıkış deliğinin kesit alanı (m2)
C0= Orifis katsayısı (Bu tip orifislerde
katsayı 0.6 alınır)
g= yerçekimi ivmesi (9.8 m/sn2)
h1= Sıvının ilk seviyesi (m)
h2= Sıvının son seviyesi (m)
D çapında silindirik bir tank h1 seviyesine kadar akıcı (Newtonian) bir sıvı ile doludur.
Bu tank altındaki d çapında bir delikten atmosfer basıncındaki bir yere açılıyor.
Bu tank ne kadar zamanda boşalır. (Tankın üstünde de atmosfere açık bir delik var)
İlk bakışta basit bir soru gibi gözüküyor. Ama hiç de öyle değil.
Çünkü sıvının üst seviyesi ile boşaltma deliği arasındaki yükseklik (h1) düştükçe çıkış deliğindeki basınç da o kadar düşeceği için çıkış debisi gittikçe azalır ve buna bağlı olarak boşalma zamanı artar.
Bu nedenle problem sıvı seviyesine bağlı bir algoritma kurularak çözülmelidir.
Yani;
Q=V/t → t= V/Q
V=A*h →

Yukarıdaki problem için oluşturulan kodlar aşağıdaki gibidir:
import math
print("dik tankın boşalması ne kadar zaman alır?")
while True:
kesit=""
d=input("tankın kesidinin bir kenar uzunluğu veya çap: ")
d=float(d)
a0=input("boşalma deliğinin alanı: ")
a0=float(a0)
h1=input("tank içindeki sıvının ilk seviyesi: ")
h1=float(h1)
h2=input("tank içindeki sıvının son seviyesi: ")
h2=float(h2)
c0=input("boşalma deliği orifis katsayısı: ")
c0=float(c0)
t=""
dairealan=""
karealan=""
kesit=input("kare(kk)/daire(dd)")
if kesit=="dd":
dairealan=math.pi*math.pow((d/2),2)
print("Daire Kesit Alanı:",dairealan)
t=dairealan*math.sqrt(2/9.8)*(math.sqrt(h1)-math.sqrt(h2))/(a0*c0)
print("tankın boşalması",t,"saniye sürer")
print("tankın boşalması",t/60,"dakika sürer.")
elif kesit=="kk":
karealan=d**2
print("Kare Kesit Alanı:",karealan)
t=karealan*math.sqrt(2/9.81)*(math.sqrt(h1)-math.sqrt(h2))/(a0*c0)
print("tankın boşalması",t,"saniye sürer")
print("tankın boşalması",t/60,"dakika sürer.")
else:
print("Geçersiz giriş.")
Yukarıdaki problemde farklı olarak tank kesit alanı da hesaba katılmıştır. Buna göre birçok kesit alanı ihtimallerii eklenmiş ve yine sonsuz döngü içinde tanımlanmıştır. Bu sayede program her yeni problem için kapanmayacaktır.
ÖRNEK PROBLEM
Çapı 6 metre ve boyu 10 metre olan bir tankın içinde bulunan sıvının seviyesi altındaki boşaltma deliğinden 7 metre yukarıdadır.
Boşaltma deliğinin çapı 15 cm olduğuna göre bu tank ne kadar sürede boşalır.
Tankın kesit alanı D=6 m => A= 28.27 m2
Boşalma deliğinin alanı d=0.15 m => A0= 0.0177 m2
Tank içindeki sıvının ilk seviyesi h1=7.3 m
Tank içindeki sıvının son seviyesi h2=0 m (Tamamen boşalacak)
Boşalma deliği orifis katsayısı C0=0.6
Yukarıda verilen t formülünden
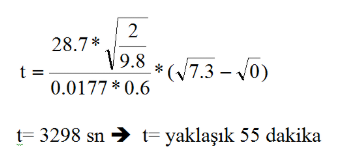
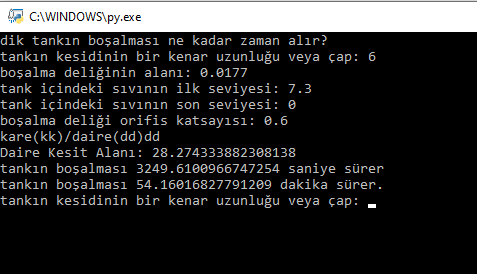
Örnek problem için program kodlarımızı doğrulayalım:
Referans
