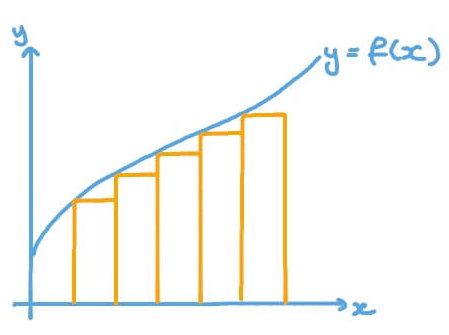
Oluşturmuş olduğum program sayesinde resimde görüleceği üzere Riemann toplamı yöntemini Python’a uyarlayarak 0-10 integral aralıklarında; kodlarda girilen fonksiyonun integralini kod çalıştırıldığında sorulan mesh değerine göre alabilirsiniz:
n=float(input('mesh: '))
m=n**4
toplam=0.0
while m<=10:
toplam=toplam+n*(m**4)
m=m+n
print (toplam)
input()
Yukarıdaki kodlara göre ilk aşamada program size belirlediğiniz mesh değerini sorar; bu değeri ne kadar küçük tutarsanız sonuç o kadar hassas şekilde hesaplanır.
m=n**4 integrali alınacak fonksiyon ifadesidir. Buradaki fonksiyonu programın kodlarına girerek değiştirebilirsin. bu ifadeyi değiştirdiğinizde aşağıdaki toplam ifadesinde de aynı fonksiyonu tekrar tanımlamanız gerekecektir.
İlk aşamada toplam float cinsinden 0.0 olarak başlar ki bu da fonksiyon alt sınırın 0 kabulü yapıldığı anlamına gelir. Daha sonra döngüde y değeri olan m’e x değerini ifade eden n değeri devamlı eklenerek m değerine atanır ve döngü integral üst sınırı 10 kabulü ile(siz bu değeri değiştirebilirsiniz.) bu şekilde toplam değere atanarak devam eder. Sonuçta toplam değer ekrana yazdırılır.
y=x^4 integrali Riemann çözümü ile ve mesh değeri sırasıyla 0.03, 0.003 ve 0.0003 kabulü ile alınır. Analitik integral bilgimize göre; y fonksiyonu integralini 0-10 sınırlarında aldığımızda; y=(x^5)/5 çıkmaktadır ve sonuç 20.000 olmaktadır. Bu analitik çözüm ile hesaplanan %100 doğru sonuçtur. Biz bu fonksiyonu kurallar olmadan nümerik olarak çözmek istediğimizde sonuç yukarıdaki mesh sıralamasına göre aşağıdaki ekran görüntülerinde görülebilir.
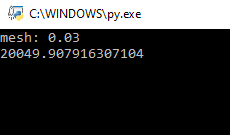


Yukarıdaki değerlerde de görüldüğü mesh değeri düşürdüğümüzde analitik yol ile ulaştığımız en doğru sonuca fazlasıyla yakınsamaktayız.
Mühendislikte analitik kullanmak çok zordur çünkü gerçek hayatta karşılan problemleri bilgisayar ortamında tasarlamak gerekir. Bu tip karmaşık problemlerde mühendisler zorlu analitik denklemleri oluşturarak zaman kaybetmektense nümerik yöntem ile bilgisayar gücünü kullanarak zamandan tasarruf sağlarlar ve analiz programlarında doğru mesh analizi gerçekleştirerek sonuca ulaşarak; tasarımlarını buna istinaden güncellerler.